Integral Curvature

Given a Geodesic Triangle (a triangle formed by the arcs of three Geodesics on a smooth surface),

$$\int_{ABC} K\,da = A+B+C-\pi.$$

Given the Euler Characteristic 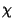$\chi$,

$$\int\!\!\!\int K\,da =2\pi\chi,$$

so the integral curvature of a closed surface is not altered by a topological transformation.

See also Gauss-Bonnet Formula, Geodesic Triangle