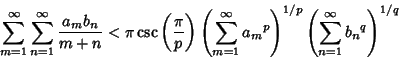Given a Positive Sequence 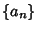 ,
,
where the 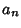 s are Real and ``square summable.''
s are Real and ``square summable.''
Another Inequality known as Hilbert's applies to Nonnegative sequences 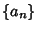 and
and 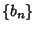 ,
,
unless all 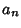 or all
or all 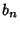 are 0. If
are 0. If 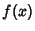 and
and 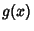 are Nonnegative integrable functions, then the integral
form is
are Nonnegative integrable functions, then the integral
form is
The constant
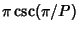 is the best possible, in the sense that counterexamples can be constructed for any
smaller value.
is the best possible, in the sense that counterexamples can be constructed for any
smaller value.
References
Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities, 2nd ed. Cambridge,
England: Cambridge University Press, pp. 308-309, 1988.
© 1996-9 Eric W. Weisstein
1999-05-25
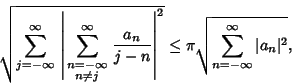
![]() and
and ![]() ,
,