|
|
|
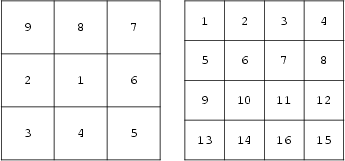
A heterosquare is an ![]() Array of the integers from 1 to
Array of the integers from 1 to ![]() such that the rows, columns, and diagonals have
different sums. (By contrast, in a Magic Square, they have the same sum.) There are no heterosquares of order
two, but heterosquares of every Odd order exist. They can be constructed by placing consecutive Integers
in a Spiral pattern (Fults 1974, Madachy 1979).
such that the rows, columns, and diagonals have
different sums. (By contrast, in a Magic Square, they have the same sum.) There are no heterosquares of order
two, but heterosquares of every Odd order exist. They can be constructed by placing consecutive Integers
in a Spiral pattern (Fults 1974, Madachy 1979).
An Antimagic Square is a special case of a heterosquare for which the sums of rows, columns, and main diagonals form a Sequence of consecutive integers.
See also Antimagic Square, Magic Square, Talisman Square
References
Duncan, D. ``Problem 86.'' Math. Mag. 24, 166, 1951.
Fults, J. L. Magic Squares. Chicago, IL: Open Court, 1974.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 101-103, 1979.
![]() Weisstein, E. W. ``Magic Squares.'' Mathematica notebook MagicSquares.m.
Weisstein, E. W. ``Magic Squares.'' Mathematica notebook MagicSquares.m.