|
|
|
A nonlinear nonintegrable Hamiltonian System with
| (1) | |||
| (2) |
| (3) | |||
| (4) |
| (5) |
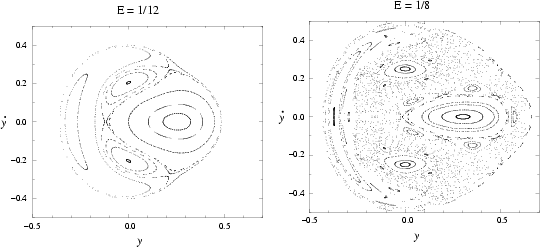
The above plots are Surfaces of Section for ![]() and
and ![]() . The Hamiltonian for a
generalized Hénon-Heiles potential is
. The Hamiltonian for a
generalized Hénon-Heiles potential is
| (6) |
References
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, pp. 144-153, 1988.
Hénon, M. and Heiles, C. ``The Applicability of the Third Integral of Motion: Some Numerical Experiments.''
Astron. J. 69, 73-79, 1964.