|
|
|
Any Vector Field ![]() satisfying
satisfying
| (1) | |||
| (2) |
| (3) |
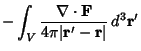 |
(4) | ||
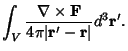 |
(5) |
See also Irrotational Field, Solenoidal Field, Vector Field
References
Arfken, G. ``Helmholtz's Theorem.'' §1.15 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 78-84, 1985.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1084, 1980.