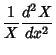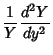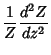In 2-D Cartesian Coordinates, attempt Separation of Variables by writing
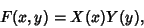 |
(1) |
then the Helmholtz Differential Equation becomes
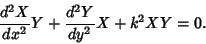 |
(2) |
Dividing both sides by 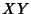 gives
gives
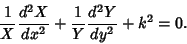 |
(3) |
This leads to the two coupled ordinary differential equations with a separation constant
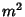 ,
,
where 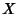 and
and 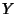 could be interchanged depending on the boundary conditions. These have solutions
could be interchanged depending on the boundary conditions. These have solutions
The general solution is then
![\begin{displaymath}
F(x, y) = \sum_{m=1}^\infty (A_me^{mx}+B_me^{-mx})[E_m\sin(\sqrt{m^2+k^2}\,y)+F_m\cos(\sqrt{m^2+k^2}\,y)].
\end{displaymath}](h_920.gif) |
(8) |
In 3-D Cartesian Coordinates, attempt Separation of Variables by writing
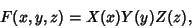 |
(9) |
then the Helmholtz Differential Equation becomes
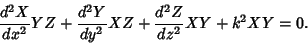 |
(10) |
Dividing both sides by 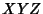 gives
gives
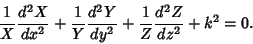 |
(11) |
This leads to the three coupled differential equations
where 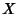 ,
, 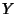 , and
, and 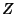 could be permuted depending on boundary conditions. The general solution is therefore
could be permuted depending on boundary conditions. The general solution is therefore
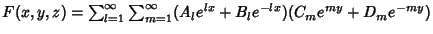
|
|
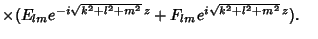
|
(15) |
References
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York:
McGraw-Hill, pp. 501-502, 513-514 and 656, 1953.
© 1996-9 Eric W. Weisstein
1999-05-25
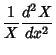
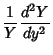
![\begin{displaymath}
F(x, y) = \sum_{m=1}^\infty (A_me^{mx}+B_me^{-mx})[E_m\sin(\sqrt{m^2+k^2}\,y)+F_m\cos(\sqrt{m^2+k^2}\,y)].
\end{displaymath}](h_920.gif)