Helicoid

The Minimal Surface having a Helix as its boundary. It is the only Ruled Minimal Surface other than the Plane (Catalan 1842, do Carmo 1986). For many years, the helicoid remained the only known example of a complete embedded Minimal Surface of finite topology with infinite Curvature. However, in 1992 a second example, known as Hoffman's Minimal Surface and consisting of a helicoid with a Hole, was discovered (Sci. News 1992).

The equation of a helicoid in Cylindrical Coordinates is

$\begin{displaymath} z=c\theta. \end{displaymath}$

(1)

In Cartesian Coordinates, it is

$\begin{displaymath} {y\over x}=\tan\left({z\over c}\right). \end{displaymath}$

(2)

It can be given in parametric form by

$\displaystyle x$	$\textstyle =$	$\displaystyle u\cos v$	(3)
$\displaystyle y$	$\textstyle =$	$\displaystyle u\sin v$	(4)
$\displaystyle z$	$\textstyle =$	$\displaystyle c u,$	(5)

which has an obvious generalization to the Elliptic Helicoid. The differentials are

$\displaystyle dx$	$\textstyle =$	$\displaystyle \cos v\,du-u\sin v\,dv$	(6)
$\displaystyle dy$	$\textstyle =$	$\displaystyle \sin v\,du+u\cos v\,dv$	(7)
$\displaystyle dz$	$\textstyle =$	$\displaystyle 2 cu\,dy,$	(8)

so the Line Element on the surface is

$\displaystyle ds^2$	$\textstyle =$	$\displaystyle dx^2+dy^2+dz^2$
	$\textstyle =$	$\displaystyle \cos^2 v\,du^2-2u \sin v\cos v\,du\,dv+u^2\sin^2 v\,dv^2$
	$\textstyle \phantom{=}$	$\displaystyle \mathop{+} \sin^2 v\,du^2+2u\sin v\cos v\,du\,dv+u^2\cos^2 v\,dv^2+4c^2u^2\,du^2$
	$\textstyle =$	$\displaystyle (1+4c^2u^2)\,du^2+u^2\,dv^2,$	(9)

and the Metric components are

$\displaystyle g_{uu}$	$\textstyle =$	$\displaystyle 1+4c^2u^2$	(10)
$\displaystyle g_{uv}$	$\textstyle =$	$\displaystyle 0$	(11)
$\displaystyle g_{vv}$	$\textstyle =$	$\displaystyle u^2.$	(12)

From Gauss's Theorema Egregium, the Gaussian Curvature is then

$\begin{displaymath} K={4c^2\over(1+4c^2 u^2)^2}. \end{displaymath}$

(13)

The Mean Curvature is

$\begin{displaymath} H=0, \end{displaymath}$

(14)

and the equation for the Lines of Curvature is

$\begin{displaymath} u=\pm c\sinh (v-k). \end{displaymath}$

(15)

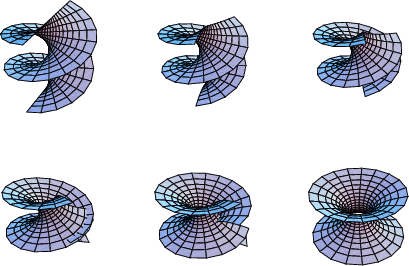
$\begin{figure}\begin{center}\BoxedEPSF{HelicoidCatenoid.epsf}\end{center}\end{figure}$

The helicoid can be continuously deformed into a Catenoid by the transformation

$\displaystyle x(u,v)$	$\textstyle =$	$\displaystyle \cos\alpha\sinh v\sin u+\sin\alpha\cosh v\cos u$	(16)
$\displaystyle y(u,v)$	$\textstyle =$	$\displaystyle -\cos\alpha\sinh v\cos u+\sin\alpha\cosh v\sin u$	(17)
$\displaystyle z(u,v)$	$\textstyle =$	$\displaystyle u\cos\alpha+v\sin\alpha,$	(18)

where $\alpha=0$ corresponds to a helicoid and $\alpha=\pi/2$ to a Catenoid.

If a twisted curve (i.e., one with Torsion $\tau\not=0$ ) rotates about a fixed axis and, at the same time, is displaced parallel to such that the speed of displacement is always proportional to the angular velocity of rotation, then generates a Generalized Helicoid.

References

Catalan E. ``Sur les surfaces réglées dont l'aire est un minimum.'' J. Math. Pure Appl. 7, 203-211, 1842.

do Carmo, M. P. ``The Helicoid.'' §3.5B in Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, pp. 44-45, 1986.

Fischer, G. (Ed.). Plate 91 in Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume. Braunschweig, Germany: Vieweg, p. 87, 1986.

Geometry Center. ``The Helicoid.'' http://www.geom.umn.edu/zoo/diffgeom/surfspace/helicoid/.

Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, p. 264, 1993.

Kreyszig, E. Differential Geometry. New York: Dover, p. 88, 1991.

Meusnier, J. B. ``Mémoire sur la courbure des surfaces.'' Mém. des savans étrangers 10 (lu 1776), 477-510, 1785.

Peterson, I. ``Three Bites in a Doughnut.'' Sci. News 127, 168, Mar. 16, 1985.

``Putting a Handle on a Minimal Helicoid.'' Sci. News 142, 276, Oct. 24, 1992.

Wolfram, S. The Mathematica Book, 3rd ed. Champaign, IL: Wolfram Media, p. 164, 1996.