Any real-valued function 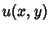 with continuous second Partial Derivatives which satisfies
Laplace's Equation
with continuous second Partial Derivatives which satisfies
Laplace's Equation
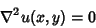 |
(1) |
is called a harmonic function. Harmonic functions are called Potential Functions in physics
and engineering. Potential functions are extremely useful, for example, in
electromagnetism,  where they reduce the study of a 3-component Vector Field to
a 1-component Scalar Function. A scalar harmonic function is called a Scalar Potential, and a vector
harmonic function is called a Vector Potential.
where they reduce the study of a 3-component Vector Field to
a 1-component Scalar Function. A scalar harmonic function is called a Scalar Potential, and a vector
harmonic function is called a Vector Potential.
To find a class of such functions in the Plane, write the Laplace's Equation in Polar Coordinates
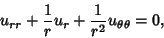 |
(2) |
and consider only radial solutions
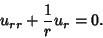 |
(3) |
This is integrable by quadrature, so define 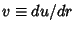 ,
,
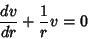 |
(4) |
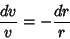 |
(5) |
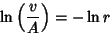 |
(6) |
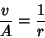 |
(7) |
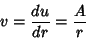 |
(8) |
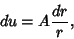 |
(9) |
so the solution is
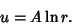 |
(10) |
Ignoring the trivial additive and multiplicative constants, the general pure radial solution then becomes
![\begin{displaymath}
u=\ln[(x-a)^2+(y-b)^2]^{1/2} = {\textstyle{1\over 2}}\ln\left[{(x-a)^2+(y-b)^2}\right].
\end{displaymath}](h_460.gif) |
(11) |
Other solutions may be obtained by differentiation, such as
and
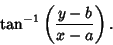 |
(16) |
Harmonic functions containing azimuthal dependence include
The Poisson Kernel
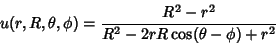 |
(19) |
is another harmonic function.
See also Scalar Potential, Vector Potential
References
 Potential Theory
Potential Theory
Ash, J. M. (Ed.) Studies in Harmonic Analysis. Washington, DC: Math. Assoc. Amer., 1976.
Axler, S.; Pourdon, P.; and Ramey, W. Harmonic Function Theory. Springer-Verlag, 1992.
Benedetto, J. J. Harmonic Analysis and Applications. Boca Raton, FL: CRC Press, 1996.
Cohn, H. Conformal Mapping on Riemann Surfaces. New York: Dover, 1980.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() with continuous second Partial Derivatives which satisfies
Laplace's Equation
with continuous second Partial Derivatives which satisfies
Laplace's Equation
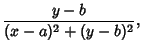
![]() Potential Theory
Potential Theory