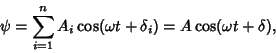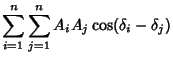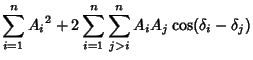To convert an equation of the form
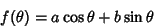 |
(1) |
to the form
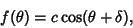 |
(2) |
expand (2) using the trigonometric addition formulas to obtain
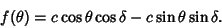 |
(3) |
Now equate the Coefficients of (1) and (3)
so
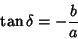 |
(6) |
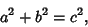 |
(7) |
and we have
Given two general sinusoidal functions with frequency 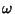 :
:
their sum 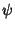 can be expressed as a sinusoidal function with frequency
can be expressed as a sinusoidal function with frequency 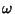
Now, define
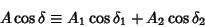 |
(13) |
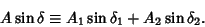 |
(14) |
Then (12) becomes
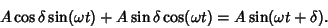 |
(15) |
Square and add (13) and (14)
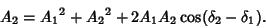 |
(16) |
Also, divide (14) by (13)
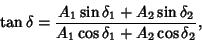 |
(17) |
so
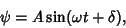 |
(18) |
where 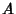 and
and 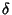 are defined by (16) and (17).
are defined by (16) and (17).
This procedure can be generalized to a sum of 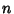 harmonic waves, giving
harmonic waves, giving
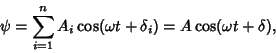 |
(19) |
where
and
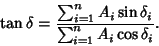 |
(22) |
© 1996-9 Eric W. Weisstein
1999-05-25
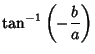
![]() harmonic waves, giving
harmonic waves, giving