|
|
|
Let ![]() be a Nonnegative Sequence and
be a Nonnegative Sequence and ![]() a Nonnegative integrable Function. Define
a Nonnegative integrable Function. Define
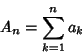 |
(1) |
| (2) |
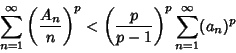 |
(3) |
| (4) |
References
Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities, 2nd ed. Cambridge,
England: Cambridge University Press, pp. 239-243, 1988.
Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M. Inequalities Involving Functions and Their Integrals and Derivatives.
New York: Kluwer, 1991.
Opic, B. and Kufner, A. Hardy-Type Inequalities. Essex, England: Longman, 1990.