Define
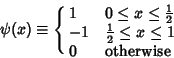 |
(1) |
and
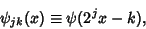 |
(2) |
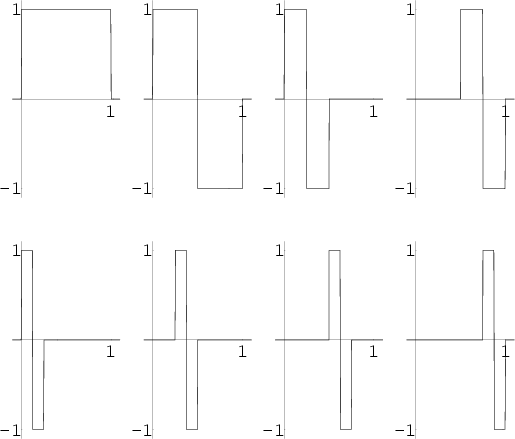
where the Functions plotted above are
Then a Function 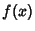 can be written as a series expansion by
can be written as a series expansion by
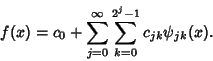 |
(3) |
The Functions 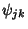 and
and 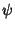 are all Orthogonal in
are all Orthogonal in ![$[0,1]$](h_60.gif) ,
with
,
with
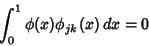 |
(4) |
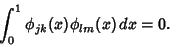 |
(5) |
These functions can be used to define Wavelets. Let a Function be defined on 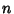 intervals,
with
intervals,
with 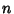 a Power of 2. Then an arbitrary function can be considered as an
a Power of 2. Then an arbitrary function can be considered as an 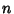 -Vector
-Vector 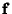 , and the
Coefficients in the expansion
, and the
Coefficients in the expansion 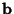 can be determined by solving the Matrix equation
can be determined by solving the Matrix equation
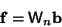 |
(6) |
for 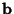 , where
, where
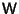 is the Matrix of
is the Matrix of 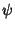 basis functions. For example,
basis functions. For example,
![\begin{displaymath}
{\hbox{\sf W}}_4 =\left[{\matrix{ 1 & \hfil 1 & \hfil 1 & \h...
...cr \hfil 1 & \hfil -1 & & \cr & & 1 & \cr & & & 1\cr}}\right].
\end{displaymath}](h_68.gif) |
(7) |
The Wavelet Matrix can be computed in
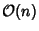 steps, compared to
steps, compared to
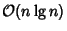 for the
Fourier Matrix.
for the
Fourier Matrix.
See also Wavelet, Wavelet Transform
References
Haar, A. ``Zur Theorie der orthogonalen Funktionensysteme.'' Math. Ann. 69, 331-371, 1910.
Strang, G. ``Wavelet Transforms Versus Fourier Transforms.'' Bull. Amer. Math. Soc. 28, 288-305, 1993.
© 1996-9 Eric W. Weisstein
1999-05-25
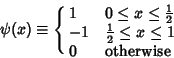
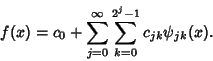
![\begin{displaymath}
{\hbox{\sf W}}_4 =\left[{\matrix{ 1 & \hfil 1 & \hfil 1 & \h...
...cr \hfil 1 & \hfil -1 & & \cr & & 1 & \cr & & & 1\cr}}\right].
\end{displaymath}](h_68.gif)