A number
where 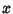 is an Integer or Rational Number,
is an Integer or Rational Number, 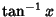 is the Inverse Tangent, and
is the Inverse Tangent, and
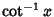 is the Inverse Cotangent. Gregory numbers arise in the determination of Machin-Like Formulas.
Every Gregory number
is the Inverse Cotangent. Gregory numbers arise in the determination of Machin-Like Formulas.
Every Gregory number 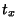 can be expressed uniquely as a sum of
can be expressed uniquely as a sum of 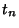 s where the
s where the 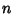 s are Størmer
Numbers.
s are Størmer
Numbers.
References
Conway, J. H. and Guy, R. K. ``Gregory's Numbers'' In The Book of Numbers. New York:
Springer-Verlag, pp. 241-242, 1996.
© 1996-9 Eric W. Weisstein
1999-05-25