|
|
|
A Labeled Graph which can be ``gracefully numbered'' is called a graceful graph. Label the nodes with distinct
Nonnegative Integers. Then label the Edges with the absolute differences
between node values. If the Edge numbers then run from 1 to ![]() , the graph is gracefully numbered. In
order for a graph to be graceful, it must be without loops or multiple Edges.
, the graph is gracefully numbered. In
order for a graph to be graceful, it must be without loops or multiple Edges.

Golomb showed that the number of Edges connecting the Even-numbered and Odd-numbered sets of nodes is
![]() , where
, where ![]() is the number of Edges. In addition, if the nodes of a graph are all of
Even Order, then the graph is graceful only if
is the number of Edges. In addition, if the nodes of a graph are all of
Even Order, then the graph is graceful only if
![]() is Even. The only ungraceful
simple graphs with
is Even. The only ungraceful
simple graphs with ![]() nodes are shown below.
nodes are shown below.
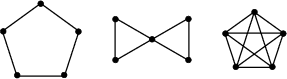
There are exactly ![]() graceful graphs with
graceful graphs with ![]() Edges (Sheppard 1976), where
Edges (Sheppard 1976), where ![]() of these correspond
to different labelings of the same graph. Golomb (1974) showed that all complete bipartite graphs are graceful.
Caterpillar Graphs; Complete Graphs
of these correspond
to different labelings of the same graph. Golomb (1974) showed that all complete bipartite graphs are graceful.
Caterpillar Graphs; Complete Graphs ![]() ,
, ![]() ,
, ![]() (and only
these; Golomb 1974); Cyclic Graphs
(and only
these; Golomb 1974); Cyclic Graphs ![]() when
when
![]() , when the number of
consecutive chords
, when the number of
consecutive chords ![]() , 3, or
, 3, or ![]() (Koh and Punnim 1982), or when they contain a
(Koh and Punnim 1982), or when they contain a ![]() chord (Delorme et al. 1980, Koh
and Yap 1985, Punnim and Pabhapote 1987); Gear Graphs; Path Graphs; the
Petersen Graph; Polyhedral Graphs
chord (Delorme et al. 1980, Koh
and Yap 1985, Punnim and Pabhapote 1987); Gear Graphs; Path Graphs; the
Petersen Graph; Polyhedral Graphs ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() (Gardner 1983); Star Graphs; the Thomsen Graph (Gardner 1983); and Wheel Graphs (Frucht 1988) are all graceful.
(Gardner 1983); Star Graphs; the Thomsen Graph (Gardner 1983); and Wheel Graphs (Frucht 1988) are all graceful.
Some graceful graphs have only one numbering, but others have more than one. It is conjectured that all trees are graceful
(Bondy and Murty 1976), but this has only been proved for trees with ![]() Vertices. It has also
been conjectured that all unicyclic graphs are graceful.
Vertices. It has also
been conjectured that all unicyclic graphs are graceful.
See also Harmonious Graph, Labeled Graph
References
Abraham, J. and Kotzig, A. ``All 2-Regular Graphs Consisting of 4-Cycles are Graceful.'' Disc. Math. 135, 1-24, 1994.
Abraham, J. and Kotzig, A. ``Extensions of Graceful Valuations of 2-Regular Graphs
Consisting of 4-Gons.'' Ars Combin. 32, 257-262, 1991.
Bloom, G. S. and Golomb, S. W. ``Applications of Numbered Unidirected Graphs.'' Proc. IEEE 65, 562-570,
1977.
Bolian, L. and Xiankun, Z. ``On Harmonious Labellings of Graphs.'' Ars Combin. 36, 315-326, 1993.
Brualdi, R. A. and McDougal, K. F. ``Semibandwidth of Bipartite Graphs and Matrices.'' Ars Combin. 30, 275-287, 1990.
Cahit, I. ``Are All Complete Binary Trees Graceful?'' Amer. Math. Monthly 83, 35-37, 1976.
Delorme, C.; Maheo, M.; Thuillier, H.; Koh, K. M.; and Teo, H. K. ``Cycles with a Chord are Graceful.''
J. Graph Theory 4, 409-415, 1980.
Frucht, R. W. and Gallian, J. A. ``Labelling Prisms.'' Ars Combin. 26, 69-82, 1988.
Gallian, J. A. ``A Survey: Recent Results, Conjectures, and Open Problems in Labelling
Graphs.'' J. Graph Th. 13, 491-504, 1989.
Gallian, J. A. ``Open Problems in Grid Labeling.'' Amer. Math. Monthly 97, 133-135, 1990.
Gallian, J. A. ``A Guide to the Graph Labelling Zoo.'' Disc. Appl. Math. 49, 213-229, 1994.
Gallian, J. A.; Prout, J.; and Winters, S. ``Graceful and Harmonious Labellings of Prism
Related Graphs.'' Ars Combin. 34, 213-222, 1992.
Gardner, M. ``Golomb's Graceful Graphs.'' Ch. 15 in Wheels, Life, and Other Mathematical Amusements.
New York: W. H. Freeman, pp. 152-165, 1983.
Golomb, S. W. ``The Largest Graceful Subgraph of the Complete Graph.'' Amer. Math. Monthly 81, 499-501, 1974.
Guy, R. ``Monthly Research Problems, 1969-75.'' Amer. Math. Monthly 82, 995-1004, 1975.
Guy, R. ``Monthly Research Problems, 1969-1979.'' Amer. Math. Monthly 86, 847-852, 1979.
Guy, R. K. ``The Corresponding Modular Covering Problem. Harmonious Labelling of Graphs.'' §C13 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 127-128, 1994.
Huang, J. H. and Skiena, S. ``Gracefully Labelling Prisms.'' Ars Combin. 38, 225-242, 1994.
Koh, K. M. and Punnim, N. ``On Graceful Graphs: Cycles with
Jungreis, D. S. and Reid, M. ``Labelling Grids.'' Ars Combin. 34, 167-182, 1992.
Koh, K. M. and Yap, K. Y. ``Graceful Numberings of Cycles with a
Moulton, D. ``Graceful Labellings of Triangular Snakes.'' Ars Combin. 28, 3-13, 1989.
Murty, U. S. R. and Bondy, J. A. Graph Theory with Applications. New York: North Holland, p. 248, 1976.
Punnim, N. and Pabhapote, N. ``On Graceful Graphs: Cycles with a
Rosa, A. ``On Certain Valuations of the Vertices of a Graph.'' In Theory of Graphs, International
Symposium, Rome, July 1966. New York: Gordon and Breach, pp. 349-355, 1967.
Sheppard, D. A. ``The Factorial Representation of Balanced Labelled Graphs.'' Discr. Math. 15, 379-388, 1976.
Sierksma, G. and Hoogeveen, H. ``Seven Criteria for Integer Sequences Being Graphic.''
J. Graph Th. 15, 223-231, 1991.
Slater, P. J. ``Note on
Snevily, H. S. ``New Families of Graphs That Have
Snevily, H. S. ``Remarks on the Graceful Tree Conjecture.'' Preprint.
Xie, L. T. and Liu, G. Z. ``A Survey of the Problem of Graceful Trees.'' Qufu Shiyuan Xuebao 1, 8-15, 1984.
![]() -Consecutive Chords.'' Bull. Malaysian Math. Soc. 5,
49-64, 1982.
-Consecutive Chords.'' Bull. Malaysian Math. Soc. 5,
49-64, 1982.
![]() -Chord.'' Bull. Inst. Math. Acad. Sinica 13, 41-48, 1985.
-Chord.'' Bull. Inst. Math. Acad. Sinica 13, 41-48, 1985.
![]() -Chord,
-Chord, ![]() .'' Ars Combin. A 23, 225-228, 1987.
.'' Ars Combin. A 23, 225-228, 1987.
![]() -Graceful, Locally Finite Graphs.'' J. Combin. Th. Ser. B 35, 319-322, 1983.
-Graceful, Locally Finite Graphs.'' J. Combin. Th. Ser. B 35, 319-322, 1983.
![]() -Labellings.'' Preprint.
-Labellings.'' Preprint.
|
|
|
© 1996-9 Eric W. Weisstein