Gosper Island

$\begin{figure}\begin{center}\BoxedEPSF{flowsnake.epsf scaled 700}\end{center}\end{figure}$

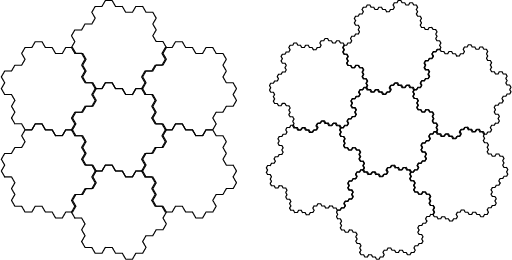
A modification of the Koch Snowflake which has Fractal Dimension

$\begin{displaymath} D={2\ln 3\over\ln 7}=1.12915\ldots. \end{displaymath}$

The term ``Gosper island'' was used by Mandelbrot (1977) because this curve bounds the space filled by the Peano-Gosper Curve; Gosper and Gardner use the term Flowsnake Fractal instead. Gosper islands can Tile the Plane.

$\begin{figure}\begin{center}\BoxedEPSF{flowsnake_tiling2.epsf scaled 850}\quad\BoxedEPSF{flowsnake_tiling3.epsf scaled 850}\end{center}\end{figure}$

See also Koch Snowflake, Peano-Gosper Curve

References

Mandelbrot, B. B. Fractals: Form, Chance, & Dimension. San Francisco, CA: W. H. Freeman, Plate 46, 1977.