Given a Hereditary Representation of a number 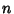 in Base, let
in Base, let $](g_1703.gif) be the
Nonnegative Integer which results if we syntactically replace each
be the
Nonnegative Integer which results if we syntactically replace each 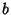 by
by 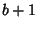 (i.e.,
(i.e., ![$B[b]$](g_1705.gif) is a base
change operator that `bumps the base' from
is a base
change operator that `bumps the base' from 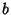 up to
up to 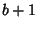 ). The Hereditary Representation of 266 in base 2 is
). The Hereditary Representation of 266 in base 2 is
so bumping the base from 2 to 3 yields
Now repeatedly bump the base and subtract 1,
etc. Starting this procedure at an Integer 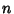 gives the Goodstein sequence
gives the Goodstein sequence 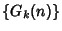 . Amazingly,
despite the apparent rapid increase in the terms of the sequence, Goodstein's Theorem states that
. Amazingly,
despite the apparent rapid increase in the terms of the sequence, Goodstein's Theorem states that
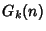 is 0 for any
is 0 for any 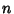 and any sufficiently large
and any sufficiently large 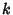 .
.
See also Goodstein's Theorem, Hereditary Representation
© 1996-9 Eric W. Weisstein
1999-05-25
![]() in Base, let
in Base, let ![]() be the
Nonnegative Integer which results if we syntactically replace each
be the
Nonnegative Integer which results if we syntactically replace each ![]() by
by ![]() (i.e.,
(i.e., ![]() is a base
change operator that `bumps the base' from
is a base
change operator that `bumps the base' from ![]() up to
up to ![]() ). The Hereditary Representation of 266 in base 2 is
). The Hereditary Representation of 266 in base 2 is