|
|
|
Let there be ![]() doctors and
doctors and ![]() patients, and let all
patients, and let all ![]() possible combinations of examinations of patients by
doctors take place. Then what is the minimum number of surgical gloves needed
possible combinations of examinations of patients by
doctors take place. Then what is the minimum number of surgical gloves needed ![]() so that no doctor must wear a glove
contaminated by a patient and no patient is exposed to a glove worn by another doctor? In this problem, the gloves can be
turned inside out and even placed on top of one another if necessary, but no ``decontamination'' of gloves is permitted.
The optimal solution is
so that no doctor must wear a glove
contaminated by a patient and no patient is exposed to a glove worn by another doctor? In this problem, the gloves can be
turned inside out and even placed on top of one another if necessary, but no ``decontamination'' of gloves is permitted.
The optimal solution is
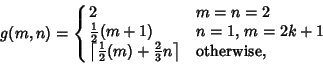
References
Gardner, M. Aha! Insight. New York: Scientific American, 1978.
Gardner, M. Science Fiction Puzzle Tales. New York: Crown, pp. 5, 67, and 104-150, 1981.
Hajnal, A. and Lovász, L. ``An Algorithm to Prevent the Propagation of Certain Diseases at Minimum Cost.''
§10.1 in Interfaces Between Computer Science and Operations Research (Ed. J. K. Lenstra, A. H. G. Rinnooy Kan,
and P. van Emde Boas). Amsterdam: Matematisch Centrum, 1978.
Orlitzky, A. and Shepp, L. ``On Curbing Virus Propagation.'' Exercise 10.2 in Technical Memo. Bell Labs, 1989.
Vardi, I. ``The Condom Problem.'' Ch. 10 in Computational Recreations in Mathematica.
Redwood City, CA: Addison-Wesley, p. 203-222, 1991.