|
|
|
If ![]() and
and
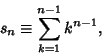
See also Argoh's Conjecture
References
Bedocchi, E. ``The
Borwein, D.; Borwein, J. M.; Borwein, P. B.; and Girgensohn, R. ``Giuga's Conjecture on Primality.''
Amer. Math. Monthly 103, 40-50, 1996.
Giuga, G. ``Su una presumibile propertietà caratteristica dei numeri primi.''
Ist. Lombardo Sci. Lett. Rend. A 83, 511-528, 1950.
Ribenboim, P. The Book of Prime Number Records, 2nd ed. New York: Springer-Verlag, pp. 20-21, 1989.
![]() Ring and the Euclidean Algorithm.'' Manuscripta Math. 53, 199-216, 1985.
Ring and the Euclidean Algorithm.'' Manuscripta Math. 53, 199-216, 1985.