|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() be a random number from
be a random number from ![]() written as a simple Continued Fraction
written as a simple Continued Fraction
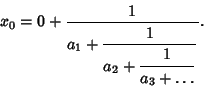 |
(1) |
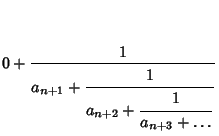 |
|||
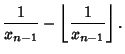 |
(2) |
| (3) |
| (4) |
References
Babenko, K. I. ``On a Problem of Gauss.'' Soviet Math. Dokl. 19, 136-140, 1978.
Daudé, H.; Flajolet, P.; and Vallée, B. ``An Average-Case Analysis of the Gaussian Algorithm for Lattice Reduction.''
Submitted.
Durner, A. ``On a Theorem of Gauss-Kuzmin-Lévy.'' Arch. Math. 58, 251-256, 1992.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/kuzmin/kuzmin.html
Flajolet, P. and Vallée, B. ``On the Gauss-Kuzmin-Wirsing Constant.'' Unpublished memo. 1995.
http://pauillac.inria.fr/algo/flajolet/Publications/gauss-kuzmin.ps.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed.
Reading, MA: Addison-Wesley, 1981.
MacLeod, A. J. ``High-Accuracy Numerical Values of the Gauss-Kuzmin Continued Fraction Problem.'' Computers
Math. Appl. 26, 37-44, 1993.
Wirsing, E. ``On the Theorem of Gauss-Kuzmin-Lévy and a Frobenius-Type Theorem for Function Spaces.'' Acta
Arith. 24, 507-528, 1974.