Let the elements in a Payoff Matrix be denoted 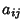 , where the
, where the 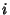 s are player A's Strategies
and the
s are player A's Strategies
and the 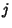 s are player B's Strategies. Player A can get at least
s are player B's Strategies. Player A can get at least
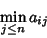 |
(1) |
for Strategy 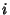 . Player B can force player A to get no more than
. Player B can force player A to get no more than
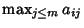 for a Strategy
for a Strategy 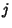 . The
best Strategy for player A is therefore
. The
best Strategy for player A is therefore
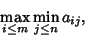 |
(2) |
and the best Strategy for player B is
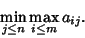 |
(3) |
In general,
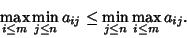 |
(4) |
Equality holds only if a Saddle Point is present, in which case the quantity is called
the Value of the game.
See also Game, Payoff Matrix, Saddle Point (Game), Strategy, Value
© 1996-9 Eric W. Weisstein
1999-05-25
![]() , where the
, where the ![]() s are player A's Strategies
and the
s are player A's Strategies
and the ![]() s are player B's Strategies. Player A can get at least
s are player B's Strategies. Player A can get at least