|
|
|
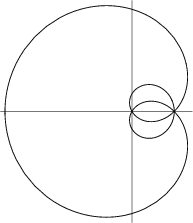
A Strophoid of a Circle with the Pole ![]() at the Center of the Circle and the fixed point
at the Center of the Circle and the fixed point ![]() on the Circumference of the Circle. In a paper published by the London Mathematical Society in 1879, T. J. Freeth
described it and various other Strophoids (MacTutor Archive). If the line through
on the Circumference of the Circle. In a paper published by the London Mathematical Society in 1879, T. J. Freeth
described it and various other Strophoids (MacTutor Archive). If the line through ![]() Parallel
to the y-Axis cuts the Nephroid at
Parallel
to the y-Axis cuts the Nephroid at ![]() , then Angle
, then Angle ![]() is
is ![]() , so this curve can be used to
construct a regular Heptagon. The Polar equation is
, so this curve can be used to
construct a regular Heptagon. The Polar equation is
See also Strophoid
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 175 and 177-178, 1972.
MacTutor History of Mathematics Archive. ``Freeth's Nephroid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Freeths.html.