A function 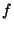 is Fréchet differentiable at
is Fréchet differentiable at 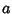 if
if
exists. This is equivalent to the statement that 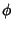 has a removable Discontinuity at
has a removable Discontinuity at 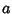 , where
, where
Every function which is Fréchet differentiable is also Carathéodory differentiable.
See also Carathéodory Derivative, Derivative
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is Fréchet differentiable at
is Fréchet differentiable at ![]() if
if