Let
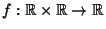 be a one-parameter family of
be a one-parameter family of 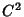 Map satisfying
Map satisfying
then there exist intervals 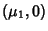 ,
, 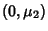 and
and 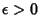 such that
such that
- 1. If
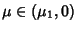 , then
, then 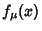 has two fixed points in
has two fixed points in
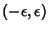 with the positive one
being unstable and the negative one stable, and
with the positive one
being unstable and the negative one stable, and
- 2. If
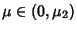 , then
, then 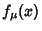 has no fixed points in
has no fixed points in
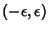 .
.
This type of Bifurcation is known as a fold bifurcation, sometimes also called a Saddle-Node Bifurcation or
Tangent Bifurcation. An example of an equation displaying a fold bifurcation is
(Guckenheimer and Holmes 1997, p. 145).
See also Bifurcation
References
Guckenheimer, J. and Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 3rd ed.
New York: Springer-Verlag, pp. 145-149, 1997.
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 27-28, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be a one-parameter family of
be a one-parameter family of ![]() Map satisfying
Map satisfying
![\begin{eqnarray*}
f(0,0)&=&0\\
\left[{\partial f\over\partial x}\right]_{\mu=...
...\\
\left[{\partial f\over\partial\mu}\right]_{\mu=0, x=0}&>&0,
\end{eqnarray*}](f_1511.gif)