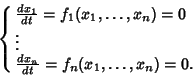Fixed Point (Differential Equations)

Points of an Autonomous system of ordinary differential equations at which

$$\cases{{dx_1\over dt}=f_1(x_1,\ldots,x_n)=0\cr \vdots\cr {dx_n\over dt}=f_n(x_1,\ldots,x_n)=0.\cr}$$

If a variable is slightly displaced from a Fixed Point, it may (1) move back to the fixed point (``asymptotically stable'' or ``superstable''), (2) move away (``unstable''), or (3) move in a neighborhood of the fixed point but not approach it (``stable'' but not ``asymptotically stable''). Fixed points are also called Critical Points or Equilibrium Points. If a variable starts at a point that is not a Critical Point, it cannot reach a critical point in a finite amount of time. Also, a trajectory passing through at least one point that is not a Critical Point cannot cross itself unless it is a Closed Curve, in which case it corresponds to a periodic solution.

A fixed point can be classified into one of several classes using Linear Stability analysis and the resulting Stability Matrix.

See also Elliptic Fixed Point (Differential Equations), Hyperbolic Fixed Point (Differential Equations), Stable Improper Node, Stable Node, Stable Spiral Point, Stable Star, Unstable Improper Node, Unstable Node, Unstable Spiral Point, Unstable Star