|
|
|
A Statistical Test used to determine if there are nonrandom associations between two Categorical
Variables. Let there exist two such variables ![]() and
and ![]() , with
, with ![]() and
and ![]() observed states,
respectively. Now form an
observed states,
respectively. Now form an ![]() Matrix in which the entries
Matrix in which the entries ![]() represent the number of observations in
which
represent the number of observations in
which ![]() and
and ![]() . Calculate the row and column sums
. Calculate the row and column sums ![]() and
and ![]() , respectively, and the total sum
, respectively, and the total sum
The test is most commonly applied to a ![]() Matrices, and is computationally unwieldy for large
Matrices, and is computationally unwieldy for large
![]() or
or ![]() .
.
For an example application of the test, let ![]() be a journal, say either Mathematics Magazine or Science, and
let
be a journal, say either Mathematics Magazine or Science, and
let ![]() be the number of articles on the topics of mathematics and biology appearing in a given issue of one of these
journals. If Mathematics Magazine has five articles on math and one on biology, and Science has none on math
and four on biology, then the relevant matrix would be
be the number of articles on the topics of mathematics and biology appearing in a given issue of one of these
journals. If Mathematics Magazine has five articles on math and one on biology, and Science has none on math
and four on biology, then the relevant matrix would be
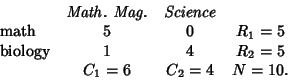
![$\displaystyle \left[\begin{array}{cc}4 & 1\\ 2 & 3\end{array}\right]\quad P$](f_1333.gif) |
|||
![$\displaystyle \left[\begin{array}{cc}3 & 2\\ 3 & 2\end{array}\right]\quad P$](f_1335.gif) |
|||
![$\displaystyle \left[\begin{array}{cc}2 & 3\\ 4 & 1\end{array}\right]\quad P$](f_1337.gif) |
|||
![$\displaystyle \left[\begin{array}{cc}1 & 4\\ 5 & 0\end{array}\right]\quad P$](f_1338.gif) |
|
|
|
© 1996-9 Eric W. Weisstein