Suppose 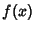 is Continuous at a Stationary Point
is Continuous at a Stationary Point 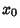 .
.
- 1. If
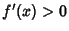 on an Open Interval extending left from
on an Open Interval extending left from 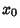 and
and 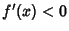 on an Open Interval
extending right from
on an Open Interval
extending right from 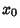 , then
, then 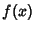 has a Relative Maximum (possibly a Global Maximum) at
has a Relative Maximum (possibly a Global Maximum) at 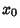 .
.
- 2. If
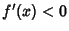 on an Open Interval extending left from
on an Open Interval extending left from 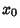 and
and 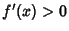 on an Open Interval extending right
from
on an Open Interval extending right
from 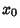 , then
, then 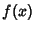 has a Relative Minimum (possibly a Global Minimum) at
has a Relative Minimum (possibly a Global Minimum) at 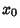 .
.
- 3. If
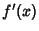 has the same sign on an Open Interval extending left from
has the same sign on an Open Interval extending left from 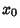 and on an Open Interval
extending right from
and on an Open Interval
extending right from 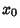 , then
, then 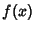 does not have a Relative Extremum at
does not have a Relative Extremum at 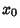 .
.
See also Extremum, Global Maximum, Global Minimum, Inflection Point, Maximum,
Minimum, Relative Extremum, Relative Maximum, Relative Minimum, Second Derivative Test,
Stationary Point
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 14, 1972.
© 1996-9 Eric W. Weisstein
1999-05-26
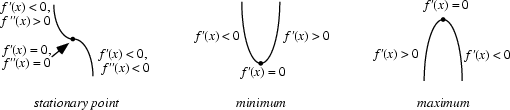
![]() is Continuous at a Stationary Point
is Continuous at a Stationary Point ![]() .
.