|
|
|
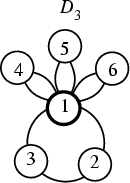
The Dihedral Group ![]() is one of the two groups of Order 6. It is the non-Abelian group of
smallest Order. Examples of
is one of the two groups of Order 6. It is the non-Abelian group of
smallest Order. Examples of ![]() include the Point Groups known as
include the Point Groups known as ![]() ,
, ![]() ,
, ![]() ,
,
![]() , the symmetry group of the Equilateral Triangle, and the group of permutation of three objects. Its elements
, the symmetry group of the Equilateral Triangle, and the group of permutation of three objects. Its elements ![]() satisfy
satisfy ![]() , and four of its elements satisfy
, and four of its elements satisfy ![]() , where 1 is the Identity Element. The Cycle
Graph is shown above, and the Multiplication Table is given below.
, where 1 is the Identity Element. The Cycle
Graph is shown above, and the Multiplication Table is given below.
| 1 | ||||||
| 1 | 1 | |||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 | ||||||
| 1 |
The Conjugacy Classes are ![]() ,
, ![]()
| (1) | |||
| (2) | |||
| (3) | |||
| (4) | |||
| (5) |
| (6) | |||
| (7) |
A reducible 2-D representation using Real Matrices can be found by performing the
spatial rotations corresponding to the symmetry elements of ![]() . Take the z-Axis along the
. Take the z-Axis along the ![]() axis.
axis.
![$\displaystyle R_z(0) = \left[\begin{array}{cc}1 & 0 \\ 0 & 1\end{array}\right]$](f_1131.gif) |
(8) | ||
![$\displaystyle R_z({\textstyle{2\over 3}}\pi)
= \left[\begin{array}{cc}\cos({\te...
...({\textstyle{2\over 3}}\pi) & \cos({\textstyle{2\over 3}}\pi)\end{array}\right]$](f_1132.gif) |
|||
![$\displaystyle \left[\begin{array}{cc}-{\textstyle{1\over 2}}& -{\textstyle{1\ov...
...}\\ {\textstyle{1\over 2}}\sqrt{3} & -{\textstyle{1\over 2}}\end{array}\right]$](f_1133.gif) |
(9) | ||
![$\displaystyle R_z({\textstyle{4\over 3}}\pi) = \left[\begin{array}{cc}-{\textst...
...\\ -{\textstyle{1\over 2}}\sqrt{3} & -{\textstyle{1\over 2}}\end{array}\right]$](f_1134.gif) |
(10) | ||
![$\displaystyle R_C(\pi) = \left[\begin{array}{cc}-1 & 0 \\ 0 & 1\end{array}\right]$](f_1135.gif) |
(11) | ||
![$\displaystyle R_D(\pi) = CB = \left[\begin{array}{cc}{\textstyle{1\over 2}}& -{...
...\\ -{\textstyle{1\over 2}}\sqrt{3} & -{\textstyle{1\over 2}}\end{array}\right]$](f_1137.gif) |
(12) | ||
![$\displaystyle R_E(\pi) = CA = \left[\begin{array}{cc}{\textstyle{1\over 2}}& {\...
...\\ {\textstyle{1\over 2}}\sqrt{3} & -{\textstyle{1\over 2}}\end{array}\right].$](f_1138.gif) |
(13) |
To find the irreducible representation, note that there are three Conjugacy Classes. Rule 5
requires that there be three irreducible representations satisfying
| (14) |
| (15) |
|
|
1 | |||||
| 1 | 1 | 1 | 1 | 1 | 1 |
To find a representation orthogonal to the totally symmetric representation, we must have three ![]() and three
and three ![]() Characters. We can also add the constraint that the components of the Identity Element 1 be
positive. The three Conjugacy Classes have 1, 2, and 3 elements. Since we need a total of three
Characters. We can also add the constraint that the components of the Identity Element 1 be
positive. The three Conjugacy Classes have 1, 2, and 3 elements. Since we need a total of three ![]() s
and we have required that a
s
and we have required that a ![]() occur for the Conjugacy Class of Order 1, the
remaining +1s must be used for the elements of the Conjugacy Class of Order 2, i.e.,
occur for the Conjugacy Class of Order 1, the
remaining +1s must be used for the elements of the Conjugacy Class of Order 2, i.e.,
![]() and
and ![]() .
.
| 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 |
Using Group rule 1, we see that
| (16) |
| (17) | |||
| (18) |
| 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||||
| 2 | 0 | 0 | 0 |
Since there are only three Conjugacy Classes, this table is conventionally written simply as
| 1 | |||
| 1 | 1 | 1 | |
| 1 | 1 | ||
| 2 | 0 |
Writing the irreducible representations in matrix form then yields
![$\displaystyle \left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right]$](f_1155.gif) |
(19) | ||
![$\displaystyle \left[\begin{array}{cccc}-{\textstyle{1\over 2}}& -{\textstyle{1\...
...extstyle{1\over 2}}& 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right]$](f_1156.gif) |
(20) | ||
![$\displaystyle \left[\begin{array}{cccc}-{\textstyle{1\over 2}}& {\textstyle{1\o...
...extstyle{1\over 2}}& 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{array}\right]$](f_1157.gif) |
(21) | ||
![$\displaystyle \left[\begin{array}{cccc}-1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1\end{array}\right]$](f_1158.gif) |
(22) | ||
![$\displaystyle \left[\begin{array}{cccc}{\textstyle{1\over 2}}& -{\textstyle{1\o...
...xtstyle{1\over 2}}& 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1\end{array}\right]$](f_1159.gif) |
(23) | ||
![$\displaystyle \left[\begin{array}{cccc}{\textstyle{1\over 2}}& {\textstyle{1\ov...
...tstyle{1\over 2}}& 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1\end{array}\right].$](f_1160.gif) |
(24) |
See also Dihedral Group, Finite Group D4, Finite Group Z6
|
|
|
© 1996-9 Eric W. Weisstein