Also known as the difference of squares. It was first used by Fermat  and improved by Gauß.
and improved by Gauß.  Gauss
looked for Integers
Gauss
looked for Integers 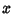 and
and 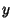 satisfying
satisfying
for various moduli 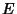 . This allowed the exclusion of many potential factors. This method works best when factors are
of approximately the same size, so it is sometimes better to attempt
. This allowed the exclusion of many potential factors. This method works best when factors are
of approximately the same size, so it is sometimes better to attempt 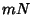 for some suitably chosen value of
for some suitably chosen value of 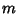 .
.
See also Prime Factorization Algorithms
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and improved by Gauß.
and improved by Gauß. ![]() Gauss
looked for Integers
Gauss
looked for Integers ![]() and
and ![]() satisfying
satisfying