The numbers 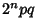 and
and 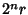 are Amicable Numbers if the three Integers
are Amicable Numbers if the three Integers
are all Prime numbers for some Positive Integer 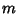 satisfying
satisfying
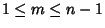 (Dickson 1952, p. 42).
However, there are exotic Amicable Numbers which do not satisfy Euler's rule,
so it is a Sufficient but not
Necessary condition for amicability.
(Dickson 1952, p. 42).
However, there are exotic Amicable Numbers which do not satisfy Euler's rule,
so it is a Sufficient but not
Necessary condition for amicability.
See also Amicable Numbers
References
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea, 1952.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
and ![]() are Amicable Numbers if the three Integers
are Amicable Numbers if the three Integers