Euclid's Theorems

A theorem sometimes called ``Euclid's First Theorem'' or Euclid's Principle states that if $p$ is a Prime and $p\vert ab$, then $p\vert a$ or $p\vert b$ (where $\vert$ means Divides). A Corollary is that $p\vert a^n \Rightarrow p\vert a$ (Conway and Guy 1996). The Fundamental Theorem of Arithmetic is another Corollary (Hardy and Wright 1979).

Euclid's Second Theorem states that the number of Primes is Infinite. This theorem, also called the Infinitude of Primes theorem, was proved by Euclid in Proposition IX.20 of the Elements. Ribenboim (1989) gives nine (and a half) proofs of this theorem. Euclid's elegant proof proceeds as follows. Given a finite sequence of consecutive Primes 2, 3, 5, ..., $p$, the number

$$N=2\cdot 3\cdot 5\cdots p+1,$$ (1)

known as the $i$th Euclid Number when $p=p_i$ is the $i$th Prime, is either a new Prime or the product of Primes. If $N$ is a Prime, then it must be greater than the previous Primes, since one plus the product of Primes must be greater than each Prime composing the product. Now, if $N$ is a product of Primes, then at least one of the Primes must be greater than $p$. This can be shown as follows. If $N$ is Composite and has no factor greater than $p$, then one of its factors (say $F$) must be one of the Primes in the sequence, 2, 3, 5, ..., $p$. It therefore Divides the product $2\cdot 3 \cdot 5\cdots p$. However, since it is a factor of $N$, it also Divides $N$. But a number which Divides two numbers $a$ and $b<a$ also Divides their difference $a-b$, so $F$ must also divide

$$N-(2\cdot 3\cdot 5\cdots p)=(2\cdot 3\cdot 5\cdots p+1)-(2\cdot 3\cdot 5\cdots p)=1.$$ (2)

However, in order to divide 1, $F$ must be 1, which is contrary to the assumption that it is a Prime in the sequence 2, 3, 5, .... It therefore follows that if $N$ is composite, it has at least one factor greater than $p$. Since $N$ is either a Prime greater than $p$ or contains a prime factor greater than $p$, a Prime larger than the largest in the finite sequence can always be found, so there are an infinite number of Primes. Hardy (1967) remarks that this proof is ``as fresh and significant as when it was discovered'' so that ``two thousand years have not written a wrinkle'' on it.

A similar argument shows that $p!\pm 1$ and

$$1\cdot 3\cdot 5\cdot 7\cdots p+1$$ (3)

must be either Prime or be divisible by a Prime $>p$. Kummer used a variation of this proof, which is also a proof by contradiction. It assumes that there exist only a finite number of Primes $N=p_1$, $p_2$, ..., $p_r$. Now consider $N-1$. It must be a product of Primes, so it has a Prime divisor $p_i$ in common with $N$. Therefore, $p_i \vert N-(N-1)=1$ which is nonsense, so we have proved the initial assumption is wrong by contradiction.

It is also true that there are runs of Composite Numbers which are arbitrarily long. This can be seen by defining

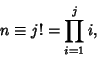$$n\equiv j!=\prod_{i=1}^j i,$$ (4)

where $j!$ is a Factorial. Then the $j-1$ consecutive numbers $n+2$, $n+3$, ..., $n+j$ are Composite, since

$$n+2 = (1\cdot 2\cdots j)+2 = 2(1\cdot 3\cdot 4\cdots n+1)$$ (5)

$$n+3 = (1\cdot 2\cdots j)+3 = 3(1\cdot 2\cdot 4\cdot 5\cdots n+1)$$ (6)

$$n+j = (1\cdot 2\cdots j)+j = j[1\cdot 2\cdots (j-1)+1].$$ (7)

Guy (1981, 1988) points out that while $p_1 p_2 \cdots p_n+1$ is not necessarily Prime, letting $q$ be the next Prime after $p_1 p_2 \cdots p_n+1$, the number $q-p_1 p_2 \cdots p_n+1$ is almost always a Prime, although it has not been proven that this must always be the case.

See also Divide, Euclid Number, Prime Number

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 60, 1987.

Conway, J. H. and Guy, R. K. ``There are Always New Primes!'' In The Book of Numbers. New York: Springer-Verlag, pp. 133-134, 1996.

Cosgrave, J. B. ``A Remark on Euclid's Proof of the Infinitude of Primes.'' Amer. Math. Monthly 96, 339-341, 1989.

Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 22, 1996.

Dunham, W. ``Great Theorem: The Infinitude of Primes.'' Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 73-75, 1990.

Guy, R. K. §A12 in Unsolved Problems in Number Theory. New York: Springer-Verlag, 1981.

Guy, R. K. ``The Strong Law of Small Numbers.'' Amer. Math. Monthly 95, 697-712, 1988.

Hardy, G. H. A Mathematician's Apology. Cambridge, England: Cambridge University Press, 1992.

Ribenboim, P. The Book of Prime Number Records, 2nd ed. New York: Springer-Verlag, pp. 3-12, 1989.