|
|
|
The ``complementary error function''
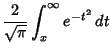 |
(1) | ||
| (2) | |||
| (3) |
| (4) | |||
| (5) |
| (6) |
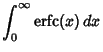 |
(7) | ||
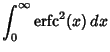 |
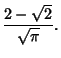 |
(8) |
A generalization is obtained from the differential equation
| (9) |
| (10) |
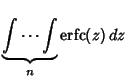 |
(11) | ||
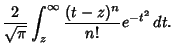 |
(12) |
| (13) | |||
| (14) |
See also Erf, Erfi
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Repeated Integrals of the Error Function.''
§7.2 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 299-300, 1972.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Incomplete Gamma Function, Error Function, Chi-Square Probability Function,
Cumulative Poisson Function.'' §6.2 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 209-214, 1992.
Spanier, J. and Oldham, K. B. ``The Error Function
![]() and Its Complement
and Its Complement
![]() '' and
``The
'' and
``The
![]() and
and
![]() and Related Functions.''
Chs. 40 and 41 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393
and 395-403, 1987.
and Related Functions.''
Chs. 40 and 41 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 385-393
and 395-403, 1987.
|
|
|
© 1996-9 Eric W. Weisstein