The Group of an Elliptic Curve which has been transformed to the form
is the set of 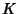 -Rational Points, including the single Point at Infinity. The group
law (addition) is defined as follows: Take 2
-Rational Points, including the single Point at Infinity. The group
law (addition) is defined as follows: Take 2 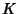 -Rational Points
-Rational Points 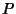 and
and 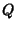 . Now `draw'
a straight line through them and compute the third point of intersection
. Now `draw'
a straight line through them and compute the third point of intersection 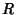 (also a
(also a 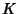 -Rational Point). Then
-Rational Point). Then
gives the identity point at infinity. Now find the inverse of 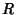 , which can be done by setting
, which can be done by setting 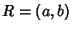 giving
giving 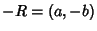 .
.
This remarkable result is only a special case of a more general procedure. Essentially, the reason is that this type of
Elliptic Curve has a single point at infinity which is an inflection point (the line at infinity meets the curve
at a single point at infinity, so it must be an intersection of multiplicity three).
© 1996-9 Eric W. Weisstein
1999-05-25