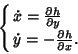The most general forced form of the Duffing equation is
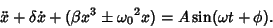 |
(1) |
If there is no forcing, the right side vanishes, leaving
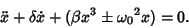 |
(2) |
If 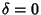 and we take the plus sign,
and we take the plus sign,
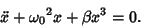 |
(3) |
This equation can display chaotic behavior. For 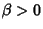 , the equation represents a ``hard spring,'' and for
, the equation represents a ``hard spring,'' and for 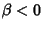 , it represents a ``soft spring.'' If
, it represents a ``soft spring.'' If 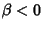 , the phase portrait curves are closed.
Returning to (1),
take
, the phase portrait curves are closed.
Returning to (1),
take 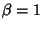 ,
, 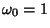 ,
, 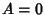 , and use the minus sign. Then the equation is
, and use the minus sign. Then the equation is
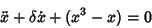 |
(4) |
(Ott 1993, p. 3). This can be written as a system of first-order
ordinary differential equations by writing
The fixed points of these differential equations
so 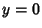 , and
, and
giving 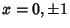 . Differentiating,
. Differentiating,
![\begin{displaymath}
\left[{\matrix{\ddot x\cr \ddot y\cr}}\right] = \left[{\matr...
...delta\cr}}\right] \left[{\matrix{\dot x\cr \dot y\cr}}\right].
\end{displaymath}](d2_1669.gif) |
(11) |
Examine the stability of the point (0,0):
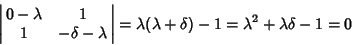 |
(12) |
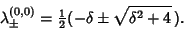 |
(13) |
But
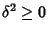 , so
, so
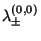 is real. Since
is real. Since
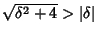 , there will always be one
Positive Root, so this fixed point is unstable. Now look at (
, there will always be one
Positive Root, so this fixed point is unstable. Now look at (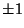 , 0).
, 0).
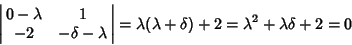 |
(14) |
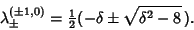 |
(15) |
For 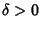 ,
,
![$\Re[\lambda^{(\pm 1,0)}_\pm] < 0$](d2_1678.gif) , so the point is asymptotically stable. If
, so the point is asymptotically stable. If 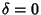 ,
,
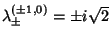 , so the point is linearly stable. If
, so the point is linearly stable. If
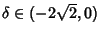 , the radical gives an
Imaginary Part and the Real Part is
, the radical gives an
Imaginary Part and the Real Part is 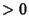 , so the point is unstable. If
, so the point is unstable. If
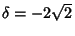 ,
,
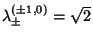 , which has a Positive Real Root, so the point is unstable. If
, which has a Positive Real Root, so the point is unstable. If
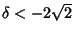 , then
, then
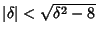 , so both Roots are Positive and the point is unstable.
The following table summarizes these results.
, so both Roots are Positive and the point is unstable.
The following table summarizes these results.
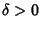 |
asymptotically stable |
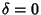 |
linearly stable (superstable) |
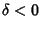 |
unstable |
Now specialize to the case 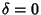 , which can be integrated by quadratures.
In this case, the equations become
, which can be integrated by quadratures.
In this case, the equations become
Differentiating (16) and plugging in (17) gives
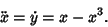 |
(18) |
Multiplying both sides by 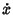 gives
gives
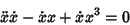 |
(19) |
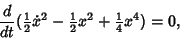 |
(20) |
so we have an invariant of motion 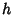 ,
,
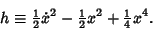 |
(21) |
Solving for 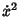 gives
gives
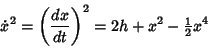 |
(22) |
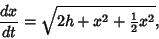 |
(23) |
so
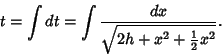 |
(24) |
Note that the invariant of motion 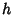 satisfies
satisfies
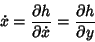 |
(25) |
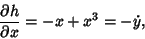 |
(26) |
so the equations of the Duffing oscillator are given by the Hamiltonian System
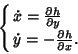 |
(27) |
References
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, 1993.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() , which can be integrated by quadratures.
In this case, the equations become
, which can be integrated by quadratures.
In this case, the equations become
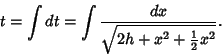
![]() satisfies
satisfies