|
|
|
![${}_3F_2\left[{\matrix{n, -x, -y\cr x+n+1, y+n+1\cr}}\right]$](d2_1335.gif)
|
|
|
|
|
|
|
(1) |
| (2) |
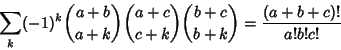 |
(3) |
See also Dougall-Ramanujan Identity, Generalized Hypergeometric Function
References
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, 1935.
Cartier, P. and Foata, D. Problèmes combinatoires de commutation et réarrangements. New York: Springer-Verlag, 1969.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1973.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, p. 43, 1996.
Zeilberger, D. and Bressoud, D. ``A Proof of Andrew's
![]() -Dyson Conjecture.'' Disc. Math. 54, 201-224, 1985.
-Dyson Conjecture.'' Disc. Math. 54, 201-224, 1985.