Write a positive decimal integer 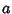 out digit by digit in the form
out digit by digit in the form
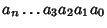 . The following rules then
determine if
. The following rules then
determine if 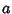 is divisible by another number by examining the Congruence properties of its digits.
is divisible by another number by examining the Congruence properties of its digits.
- 2.
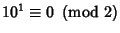 , so
, so
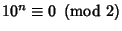 for
for 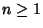 . Therefore, if the last digit
. Therefore, if the last digit 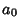 is divisible by 2
(i.e., is Even), then so is
is divisible by 2
(i.e., is Even), then so is 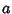 .
.
- 3.
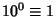 ,
, 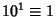 ,
, 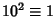 , ...,
, ..., 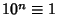 (mod 3). Therefore, if
(mod 3). Therefore, if
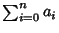 is divisible by 3, so is
is divisible by 3, so is 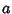 .
.
- 4.
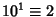 ,
, 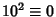 , ...
, ...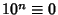 (mod 4). So if the last two digits are divisible by 4, more
specifically if
(mod 4). So if the last two digits are divisible by 4, more
specifically if
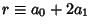 is, then so is
is, then so is 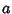 .
.
- 5.
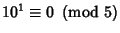 , so
, so
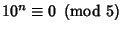 for
for 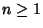 . Therefore, if the last digit
. Therefore, if the last digit 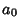 is divisible by 5 (i.e.,
is 5 or 0), then so is
is divisible by 5 (i.e.,
is 5 or 0), then so is 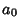 .
.
- 6.
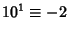 ,
, 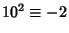 , ...,
, ..., 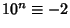 (mod 6). Therefore, if
(mod 6). Therefore, if
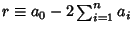 is
divisible by 6, so is
is
divisible by 6, so is 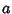 . A simpler rule states that if
. A simpler rule states that if 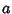 is divisible by 3 and is Even, then
is divisible by 3 and is Even, then 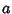 is also divisible by 6.
is also divisible by 6.
- 7.
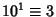 ,
, 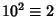 ,
, 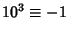 ,
, 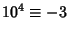 ,
,
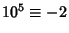 ,
, 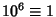 (mod 7), and the
sequence then repeats. Therefore, if
(mod 7), and the
sequence then repeats. Therefore, if
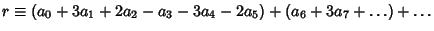 is divisible by 7, so
is
is divisible by 7, so
is 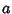 .
.
- 8.
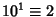 ,
, 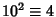 ,
, 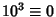 , ...,
, ..., 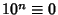 (mod 8). Therefore, if the last three digits
are divisible by 8, more specifically if
(mod 8). Therefore, if the last three digits
are divisible by 8, more specifically if
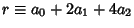 is, then so is
is, then so is 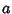 .
.
- 9.
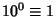 ,
, 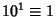 ,
, 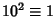 , ...,
, ..., 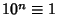 (mod 9). Therefore, if
(mod 9). Therefore, if
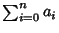 is divisible by 9,
so is
is divisible by 9,
so is 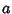 .
.
- 10.
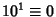 (mod 10), so if the last digit is 0, then
(mod 10), so if the last digit is 0, then 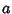 is divisible by 10.
is divisible by 10.
- 11.
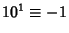 ,
, 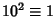 ,
, 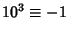 ,
, 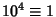 , ... (mod 11). Therefore, if
, ... (mod 11). Therefore, if
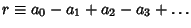 is divisible by 11, then so is
is divisible by 11, then so is 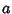 .
.
- 12.
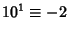 ,
, 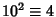 ,
, 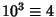 , ... (mod 12). Therefore, if
, ... (mod 12). Therefore, if
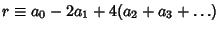 is divisible by 12, then so is
is divisible by 12, then so is 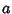 . Divisibility by 12 can also be checked by seeing if
. Divisibility by 12 can also be checked by seeing if 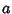 is divisible by 3 and
4.
is divisible by 3 and
4.
- 13.
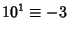 ,
, 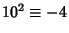 ,
, 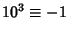 ,
, 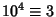 ,
, 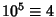 ,
, 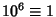 (mod 13), and the
pattern repeats. Therefore, if
(mod 13), and the
pattern repeats. Therefore, if
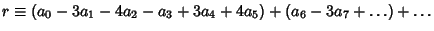 is divisible by 13, so is
is divisible by 13, so is
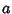 .
.
For additional tests for 13, see Gardner (1991).
References
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea,
pp. 337-346, 1952.
Gardner, M. Ch. 14 in The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University
Press, 1991.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() out digit by digit in the form
out digit by digit in the form
![]() . The following rules then
determine if
. The following rules then
determine if ![]() is divisible by another number by examining the Congruence properties of its digits.
is divisible by another number by examining the Congruence properties of its digits.