|
|
|
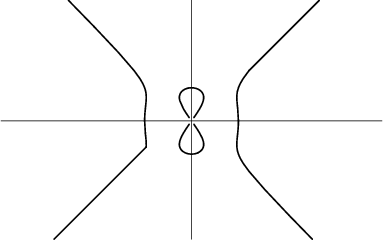
The devil's curve was studied by G. Cramer in 1750 and Lacroix in 1810 (MacTutor Archive). It appeared in Nouvelles Annales
in 1858. The Cartesian equation is
| (1) |
| (2) |
| (3) |
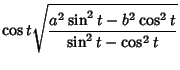 |
(4) | ||
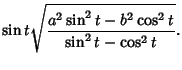 |
(5) |
A special case of the Devil's curve is the so-called Electric Motor Curve:
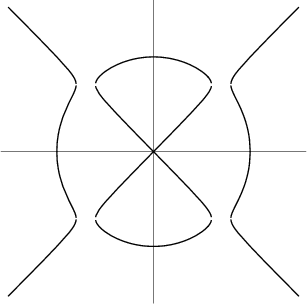
| (6) |
See also Electric Motor Curve
References
Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 71, 1989.
Gray, A. Modern Differential Geometry of Curves and Surfaces. Boca Raton, FL: CRC Press, p. 71, 1993.
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 151-152, 1972.
MacTutor History of Mathematics Archive. ``Devil's Curve.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Devils.html.