Crystallography Restriction

If a discrete Group of displacements in the plane has more than one center of rotation, then the only rotations that can occur are by 2, 3, 4, and 6. This can be shown as follows. It must be true that the sum of the interior angles divided by the number of sides is a divisor of 360°.

$${180^\circ(n-2)\over n} = {360^\circ\over m},$$

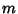where $m$ is an Integer. Therefore, symmetry will be possible only for

$${2n\over n-2} = m,$$

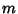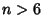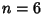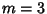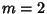where $m$ is an Integer. This will hold for 1-, 2-, 3-, 4-, and 6-fold symmetry. That it does not hold for $n > 6$ is seen by noting that $n = 6$ corresponds to $m = 3$. The $m = 2$ case requires that 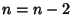$n = n-2$ (impossible), and the 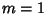$m = 1$ case requires that 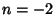$n = -2$ (also impossible).

See also Point Groups, Symmetry