|
|
|
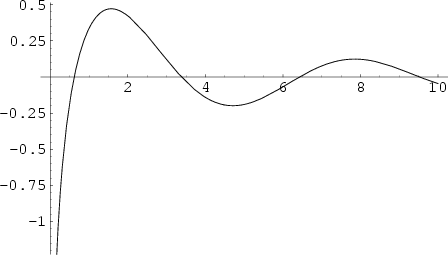
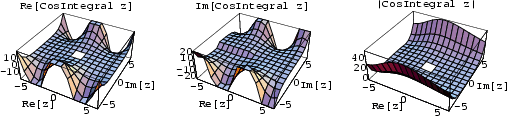
There are (at least) three types of ``cosine integrals,'' denoted
![]() ,
,
![]() , and
, and
![]() :
:
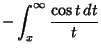 |
(1) | ||
| (2) | |||
| (3) | |||
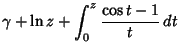 |
(4) | ||
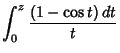 |
(5) | ||
| (6) |
To compute the integral of an Even power times a cosine,
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(13) |
|
|
|
|
|
|
|
|
|
|
|
(14) |
To find a closed form for an integral power of a cosine function,
| (15) |
| (16) |
| (17) |
|
|
|
|
|
|
|
|
(18) |
| (19) |
| (20) |
Now, if ![]() is Even so
is Even so ![]() , then
, then
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(21) |
|
|
|
|
|
(22) |
Now if ![]() is Odd so
is Odd so ![]() , then
, then
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(23) |
Now let ![]() ,
,
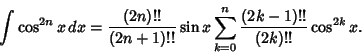 |
(24) |
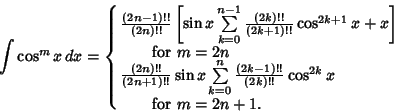 |
(25) |
The infinite integral of a cosine times a Gaussian can also be done in closed form,
| (26) |
See also Chi, Damped Exponential Cosine Integral, Nielsen's Spiral, Shi, Sici Spiral, Sine Integral
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Sine and Cosine Integrals.'' §5.2 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 231-233, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 342-343, 1985.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Fresnel Integrals, Cosine and Sine Integrals.'' §6.79 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 248-252, 1992.
Spanier, J. and Oldham, K. B. ``The Cosine and Sine Integrals.'' Ch. 38 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 361-372, 1987.
|
|
|
© 1996-9 Eric W. Weisstein