|
|
|
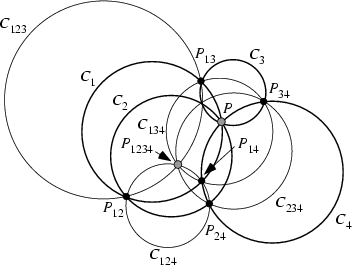
Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() be four Circles of General Position through a point
be four Circles of General Position through a point ![]() . Let
. Let
![]() be the second intersection of the Circles
be the second intersection of the Circles ![]() and
and ![]() . Let
. Let ![]() be the Circle
be the Circle
![]() . Then the four Circles
. Then the four Circles ![]() ,
, ![]() ,
, ![]() , and
, and ![]() all pass through
the point
all pass through
the point ![]() . Similarly, let
. Similarly, let ![]() be a fifth Circle through
be a fifth Circle through ![]() . Then the five points
. Then the five points ![]() ,
,
![]() ,
, ![]() ,
, ![]() and
and ![]() all lie on one Circle
all lie on one Circle ![]() . And so on.
. And so on.
See also Circle, Cox's Theorem, Miquel's Theorem, Pivot Theorem