|
|
|
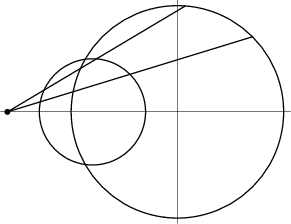
Taking the locus of Midpoints from a fixed point to a circle
of radius ![]() results in a circle of
radius
results in a circle of
radius ![]() . This follows trivially from
. This follows trivially from
![\begin{eqnarray*}
{\bf r}(\theta)&=&\left[\begin{array}{c}-x\\ 0\end{array}\rig...
...\over 2}}x\\ {\textstyle{1\over 2}}\sin\theta\end{array}\right].
\end{eqnarray*}](c2_53.gif)
References
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA:
Houghton Mifflin, p. 17, 1929.