If 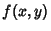 is an Analytic Function in a Neighborhood of the point
is an Analytic Function in a Neighborhood of the point 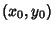 (i.e., it can be expanded in
a series of Nonnegative Integer Powers of
(i.e., it can be expanded in
a series of Nonnegative Integer Powers of 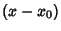 and
and 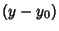 ), find a solution
), find a solution 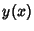 of the Differential Equation
of the Differential Equation
with initial conditions 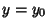 and
and 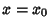 . The existence and uniqueness of the solution were proven by Cauchy
. The existence and uniqueness of the solution were proven by Cauchy  and Kovalevskaya
and Kovalevskaya  in the Cauchy-Kovalevskaya Theorem. The Cauchy problem amounts to determining the
shape of the boundary and type of equation which yield unique and reasonable solutions for the Cauchy Boundary
Conditions.
in the Cauchy-Kovalevskaya Theorem. The Cauchy problem amounts to determining the
shape of the boundary and type of equation which yield unique and reasonable solutions for the Cauchy Boundary
Conditions.
See also Cauchy Boundary Conditions
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is an Analytic Function in a Neighborhood of the point
is an Analytic Function in a Neighborhood of the point ![]() (i.e., it can be expanded in
a series of Nonnegative Integer Powers of
(i.e., it can be expanded in
a series of Nonnegative Integer Powers of ![]() and
and ![]() ), find a solution
), find a solution ![]() of the Differential Equation
of the Differential Equation