|
|
|
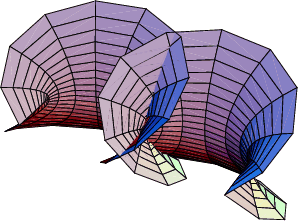
A Minimal Surface given by the parametric equations
| (1) | |||
| (2) | |||
| (3) |
| (4) | |||
| (5) | |||
| (6) |
| (7) |
References
Catalan, E. ``Mémoire sur les surfaces dont les rayons de courbures en chaque point, sont égaux et les
signes contraires.'' C. R. Acad. Sci. Paris 41, 1019-1023, 1855.
do Carmo, M. P. ``Catalan's Surface'' §3.5D in
Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer).
Braunschweig, Germany: Vieweg, pp. 45-46, 1986.
Fischer, G. (Ed.). Plates 94-95 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, pp. 90-91, 1986.
Gray, A. Modern Differential Geometry of Curves and Surfaces.Boca Raton, FL: CRC Press, pp. 448-449, 1993.