Cartesian Ovals

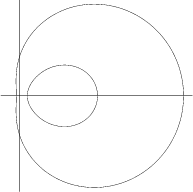
$\begin{figure}\begin{center}\BoxedEPSF{CartesianOvals.epsf scaled 600}\end{center}\end{figure}$

A curve consisting of two ovals which was first studied by Descartes in 1637. It is the locus of a point whose distances from two Foci and in two-center Bipolar Coordinates satisfy

$\begin{displaymath} mr\pm nr'=k, \end{displaymath}$

(1)

where

are Positive Integers,

is a Positive real, and

and

are the distances from

and

. If

, the oval becomes an Ellipse. In Cartesian Coordinates, the Cartesian ovals can be written

$\begin{displaymath} m\sqrt{(x-a)^2+y^2}+n\sqrt{(x+a)^2+y^2}=k^2 \end{displaymath}$

(2)

$\begin{displaymath} (x^2+y^2+a^2)(m^2-n^2)-2ax(m^2+n^2)-k^2=-2n\sqrt{(x+a)^2+y^2}, \end{displaymath}$

(3)


$= 2(m^2+n^2)(n^2+y^2+a^2)-4ax(m^2-n^2)-k^2.\quad$	(4)

Now define

$\displaystyle b$	$\textstyle \equiv$	$\displaystyle m^2-n^2$	(5)
$\displaystyle c$	$\textstyle \equiv$	$\displaystyle m^2+n^2,$	(6)

and set

. Then

$\begin{displaymath}[b(x^2+y^2)-2cx+b]^2+4bx+k^2-2c=2c(x^2+y^2). \end{displaymath}$

(7)

is the distance between

and

, and the equation

$\begin{displaymath} r+mr'=a \end{displaymath}$

(8)

is used instead, an alternate form is

$\begin{displaymath}[(1-m^2)(x^2+y^2)+2m^2c'x+a'^2-m^2c'^2]^2=4a'^2(x^2+y^2). \end{displaymath}$

(9)

The curves possess three Foci. If

, one Cartesian oval is a central Conic, while if

, then the curve is a Limaçon and the inside oval touches the outside one. Cartesian ovals are Anallagmatic Curves.

References

Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., p. 35, 1989.

Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 155-157, 1972.

Lockwood, E. H. A Book of Curves. Cambridge, England: Cambridge University Press, p. 188, 1967.

MacTutor History of Mathematics Archive. ``Cartesian Oval.'' http://www-groups.dcs.st-and.ac.uk/~history/Curves/Cartesian.html.