|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Assume that ![]() is a Nonnegative Real function on
is a Nonnegative Real function on ![]() and that the two
integrals
and that the two
integrals
| (1) |
| (2) |
| (3) |
| (4) |
![\begin{displaymath}
C={1\over(ps)^s(qt)^t}
\left[{\Gamma\left({s\over\alpha}\rig...
...lambda+\mu)\Gamma\left({s+t\over\alpha}\right)}\right]^\alpha,
\end{displaymath}](c1_187.gif) |
(5) |
| (6) | |||
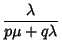 |
(7) | ||
| (8) |
References
Beckenbach, E. F.; and Bellman, R. Inequalities. New York: Springer-Verlag, 1983.
Boas, R. P. Jr. Review of Levin, V. I. ``Exact Constants in Inequalities of the Carlson Type.'' Math. Rev. 9, 415, 1948.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/crlslvn/crlslvn.html
Levin, V. I. ``Exact Constants in Inequalities of the Carlson Type.'' Doklady Akad. Nauk. SSSR (N. S.)
59, 635-638, 1948. English review in Boas (1948).
Mitrinovic, D. S.; Pecaric, J. E.; and Fink, A. M. Inequalities Involving Functions and Their
Integrals and Derivatives. Kluwer, 1991.
|
|
|
© 1996-9 Eric W. Weisstein