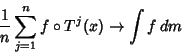Let 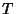 be an ergodic Endomorphism of the Probability Space
be an ergodic Endomorphism of the Probability Space 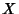 and let
and let
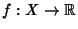 be a real-valued Measurable Function. Then for Almost Every
be a real-valued Measurable Function. Then for Almost Every 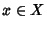 , we have
, we have
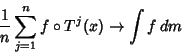 |
(1) |
as
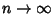 . To illustrate this, take
. To illustrate this, take 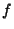 to be the characteristic function of some Subset
to be the characteristic function of some Subset 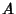 of
of 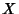 so that
so that
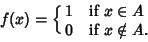 |
(2) |
The left-hand side of (1) just says how often the orbit of 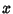 (that is, the points
(that is, the points 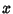 ,
, 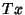 ,
, 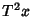 , ...)
lies in
, ...)
lies in 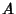 , and the right-hand side is just the Measure of
, and the right-hand side is just the Measure of 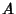 . Thus, for an ergodic Endomorphism,
``space-averages = time-averages almost everywhere.'' Moreover, if
. Thus, for an ergodic Endomorphism,
``space-averages = time-averages almost everywhere.'' Moreover, if 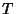 is continuous and uniquely ergodic with
Borel Probability Measure
is continuous and uniquely ergodic with
Borel Probability Measure 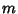 and
and 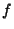 is continuous, then we can replace the Almost Everywhere convergence
in (1) to everywhere.
is continuous, then we can replace the Almost Everywhere convergence
in (1) to everywhere.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() be an ergodic Endomorphism of the Probability Space
be an ergodic Endomorphism of the Probability Space ![]() and let
and let
![]() be a real-valued Measurable Function. Then for Almost Every
be a real-valued Measurable Function. Then for Almost Every ![]() , we have
, we have