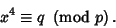 |
(1) |
This was solved by Gauß  using the Gaussian Integers as
using the Gaussian Integers as
![\begin{displaymath}
\left({\pi\over\sigma}\right)_4\left({\sigma\over\pi}\right)_4=(-1)^{[(N(\pi)-1)/4][(N(\sigma)-1)/4]},
\end{displaymath}](b_1507.gif) |
(2) |
where 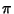 and
and 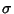 are distinct Gaussian Integer Primes,
are distinct Gaussian Integer Primes,
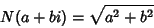 |
(3) |
and 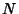 is the norm.
is the norm.
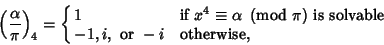 |
(4) |
where solvable means solvable in terms of Gaussian Integers.
See also Reciprocity Theorem
© 1996-9 Eric W. Weisstein
1999-05-26