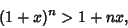 |
(1) |
where
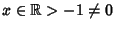 ,
,
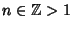 . This inequality can be proven by taking a Maclaurin Series
of
. This inequality can be proven by taking a Maclaurin Series
of 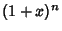 ,
,
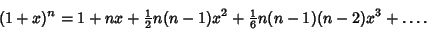 |
(2) |
Since the series terminates after a finite number of terms for Integral 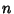 , the Bernoulli inequality
for
, the Bernoulli inequality
for 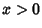 is obtained by truncating after the first-order term. When
is obtained by truncating after the first-order term. When 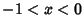 , slightly more finesse is needed. In this
case, let
, slightly more finesse is needed. In this
case, let 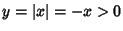 so that
so that 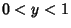 , and take
, and take
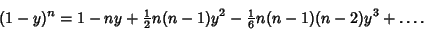 |
(3) |
Since each Power of 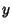 multiplies by a number
multiplies by a number 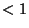 and since the Absolute Value of the Coefficient of
each subsequent term is smaller than the last, it follows that the sum of the third order and subsequent terms is a Positive
number. Therefore,
and since the Absolute Value of the Coefficient of
each subsequent term is smaller than the last, it follows that the sum of the third order and subsequent terms is a Positive
number. Therefore,
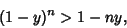 |
(4) |
or
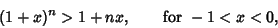 |
(5) |
completing the proof of the Inequality over all ranges of parameters.
© 1996-9 Eric W. Weisstein
1999-05-26