|
|
|
A Notation invented by Knuth (1976) to represent Large Numbers in which evaluation proceeds from the right (Conway and Guy 1996, p. 60).
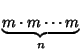 |
|
|
|
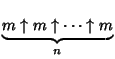 |
|
|
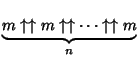 |
For example,
| (1) | |||
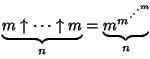 |
|||
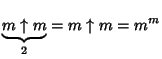 |
(2) | ||
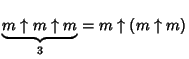 |
|||
| (3) | |||
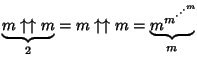 |
(4) | ||
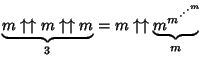 |
|||
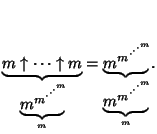 |
(5) |
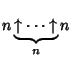 are
called Ackermann Numbers.
are
called Ackermann Numbers.
See also Ackermann Number, Chained Arrow Notation, Down Arrow Notation, Large Number, Power Tower, Steinhaus-Moser Notation
References
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 59-62, 1996.
Guy, R. K. and Selfridge, J. L. ``The Nesting and Roosting Habits of the Laddered Parenthesis.'' Amer. Math. Monthly
80, 868-876, 1973.
Knuth, D. E. ``Mathematics and Computer Science: Coping with Finiteness. Advances in Our Ability to Compute are
Bringing Us Substantially Closer to Ultimate Limitations.'' Science 194, 1235-1242, 1976.
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 11
and 226-229, 1991.