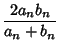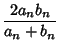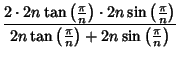Let 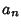 and
and 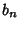 be the Perimeters of the Circumscribed and
Inscribed
be the Perimeters of the Circumscribed and
Inscribed 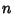 -gon and
-gon and 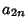 and
and 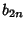 the Perimeters of the
Circumscribed and Inscribed
the Perimeters of the
Circumscribed and Inscribed 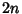 -gon. Then
-gon. Then
The first follows from the fact that side lengths of the Polygons on
a Circle of Radius 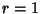 are
are
so
But
Using the identity
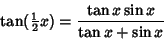 |
(8) |
then gives
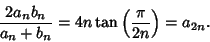 |
(9) |
The second follows from
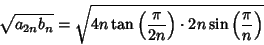 |
(10) |
Using the identity
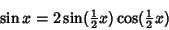 |
(11) |
gives
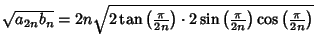
|
|
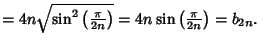
|
(12) |
Successive application gives the Archimedes Algorithm, which can be used to provide successive approximations
to Pi (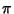 ).
).
See also Archimedes Algorithm, Pi
References
Dörrie, H. 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover,
p. 186, 1965.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() and
and ![]() be the Perimeters of the Circumscribed and
Inscribed
be the Perimeters of the Circumscribed and
Inscribed ![]() -gon and
-gon and ![]() and
and ![]() the Perimeters of the
Circumscribed and Inscribed
the Perimeters of the
Circumscribed and Inscribed ![]() -gon. Then
-gon. Then