Let 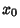 be a Rational Number in the Closed Interval
be a Rational Number in the Closed Interval ![$[0,1]$](0_10.gif) , and generate a Sequence using the
Map
, and generate a Sequence using the
Map
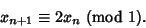 |
(1) |
Then the number of periodic Orbits of period 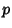 (for
(for 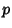 Prime) is given by
Prime) is given by
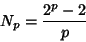 |
(2) |
(i.e, the number of period-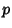 repeating bit strings, modulo shifts). Since a typical Orbit visits
each point with equal probability, the Natural Invariant is given by
repeating bit strings, modulo shifts). Since a typical Orbit visits
each point with equal probability, the Natural Invariant is given by
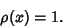 |
(3) |
See also Tent Map
References
Ott, E. Chaos in Dynamical Systems. Cambridge: Cambridge University Press, pp. 26-31, 1993.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be a Rational Number in the Closed Interval
be a Rational Number in the Closed Interval ![]() , and generate a Sequence using the
Map
, and generate a Sequence using the
Map