|
|
|
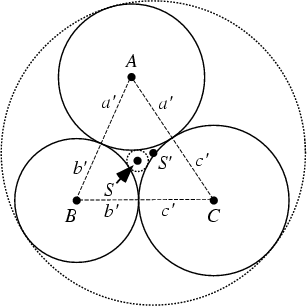
Given three distinct points ![]() ,
, ![]() , and
, and ![]() , let three Circles be drawn, one centered about each point and
each one tangent to the other two. Call the Radii
, let three Circles be drawn, one centered about each point and
each one tangent to the other two. Call the Radii ![]() (
(![]() ,
, ![]() ,
, ![]() ). Then the
Circles satisfy
). Then the
Circles satisfy
| (1) |
| (2) |
| (3) |
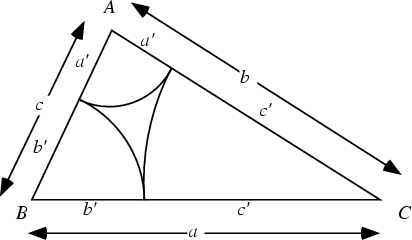
Solving for the Radii then gives
| (4) | |||
| (5) | |||
| (6) |
The above Triangle has sides ![]() ,
, ![]() , and
, and ![]() , and Semiperimeter
, and Semiperimeter
| (7) |
| (8) |
| (9) |
| (10) |
| (11) | |||
| (12) | |||
| (13) |
As can be seen from the first figure, there exist exactly two nonintersecting Circles which are
Tangent to all three Circles. These are called the inner and outer Soddy circles (![]() and
and ![]() ,
respectively), and their centers are called the inner and outer Soddy Points.
,
respectively), and their centers are called the inner and outer Soddy Points.
The inner Soddy circle is the solution to the Four Coins Problem. The center ![]() of the inner Soddy circle is the
Equal Detour Point, and the center of the outer Soddy circle
of the inner Soddy circle is the
Equal Detour Point, and the center of the outer Soddy circle ![]() is the Isoperimetric Point (Kimberling 1994).
is the Isoperimetric Point (Kimberling 1994).
Frederick Soddy (1936) gave the Formula for finding the Radii of the Soddy circles (![]() ) given the
Radii
) given the
Radii ![]() (
(![]() , 2, 3) of the other three. The relationship is
, 2, 3) of the other three. The relationship is
| (14) |
| (15) |
This Formula is called the Descartes Circle Theorem since it was known to Descartes. ![]() However, Soddy
also extended it to Spheres. Gosper has further extended the result to
However, Soddy
also extended it to Spheres. Gosper has further extended the result to ![]() mutually tangent
mutually tangent ![]() -D
Hyperspheres, whose Curvatures satisfy
-D
Hyperspheres, whose Curvatures satisfy
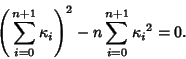 |
(16) |
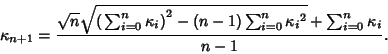 |
(17) |
For (at least) ![]() and 3, the Radical equals
and 3, the Radical equals
| (18) |
Bellew has derived a generalization applicable to a Circle surrounded by ![]() Circles which are, in
turn, circumscribed by another Circle. The relationship is
Circles which are, in
turn, circumscribed by another Circle. The relationship is
|
|
|
|
|
(19) |
| (20) |
See also Apollonius Circles, Apollonius' Problem, Arbelos, Bend (Curvature), Circumcircle, Descartes Circle Theorem, Four Coins Problem, Hart's Theorem, Pappus Chain, Sphere Packing, Steiner Chain
References
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 13-14, 1969.
Elkies, N. D. and Fukuta, J. ``Problem E3236 and Solution.'' Amer. Math. Monthly 97, 529-531, 1990.
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67, p. 181, 1994.
``The Kiss Precise.'' Nature 139, 62, 1937.
Soddy, F. ``The Kiss Precise.'' Nature 137, 1021, 1936.
Vandeghen, A. ``Soddy's Circles and the De Longchamps Point of a Triangle.'' Amer. Math. Monthly 71, 176-179, 1964.
|
|
|
© 1996-9 Eric W. Weisstein